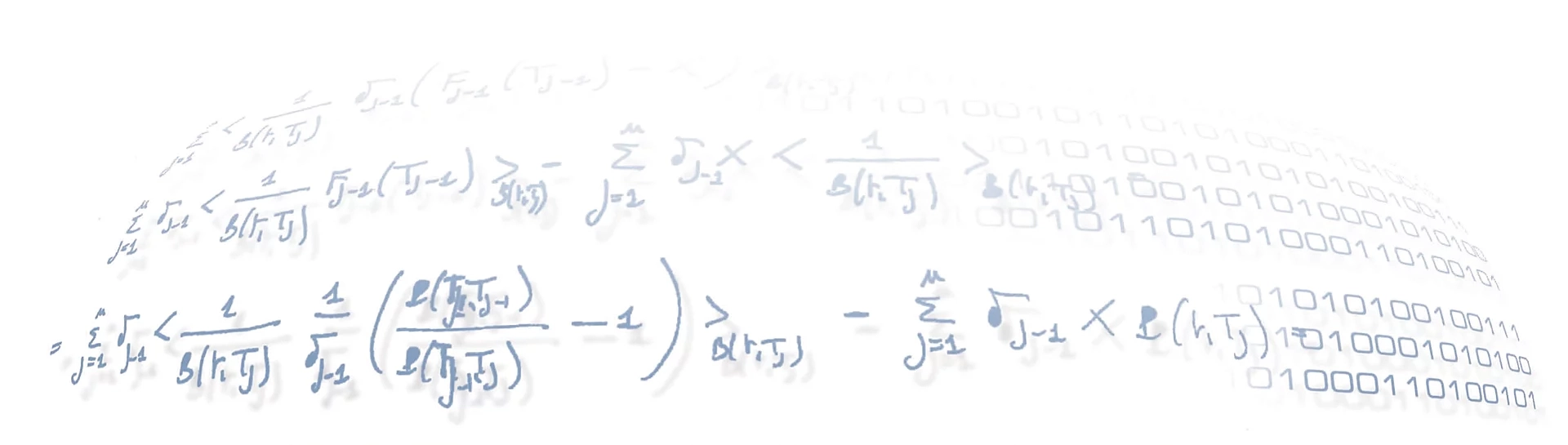2.1 Volume curve construction

The historical daily volume profiles represent how many shares are traded per day.

As said in the introductory post, during trade execution large orders are usually broken up into smaller trades for the purpose of avoiding or, at least, limiting market impact. In our simulations we have followed the same policy, splitting each order we have dealt with, of total size $Q$, into a certain number of child orders with fixed volume $q$, following a specific volume curve between the order start and end times (the different volume profiles used for our analysis are specified in Sec. 3.1 of the next post). The method adopted to partition each order at hand is explained below:

• build the cumulative volume curve on the order date for the corresponding ISIN, which represents the cumulated traded quantity from 0, at the beginning of the day, to 1, at the end of the day;
• cut this curve between the start and end times of the order and divide the ordinate interval of the resulting curve portion into $n$ equal parts, where $n$ is the result of the integer division between $Q$ and $q$;
• find the corresponding abscissa values, $t_0$, $t_1$,…, $t_n$, which indicate the times within which each child order must be executed. The times $t_i$ are such that in each interval $[t_i, t_{i+1}]$ the same quantity is exchanged; hence, the order intervals are “equal realised volume intervals”.

2.2 Market VWAP calculation

Volume-weighted average price (VWAP) is a measure of the average price at which a stock is traded over a particular time horizon (usually one day). It is calculated as the ratio of the traded value of the stock to the total volume executed over the trading horizon (see Berkowitz, Logue and Noser). As mentioned in the previous post, VWAP is commonly used by investors as a benchmark for their trade prices, in the sense that purchases with prices that are high relative to this price baseline are considered expensive trades as are sales at prices below the benchmark price.

In our analysis, for each order at issue we have computed the volume-weighted average price of its total executions between the start and end times as:

${\rm VWAP}_{\rm market} = \frac{\sum_t q_t\cdot p_t}{\sum_t q_t}$,

where $q_t$ and $p_t$ are respectively the volume and price of each market execution, produced at time $t$.

The elements given here will be helpful to better understand some passages of the following posts, where we will present our experiments in applying RL techniques to the financial problem of optimal execution.