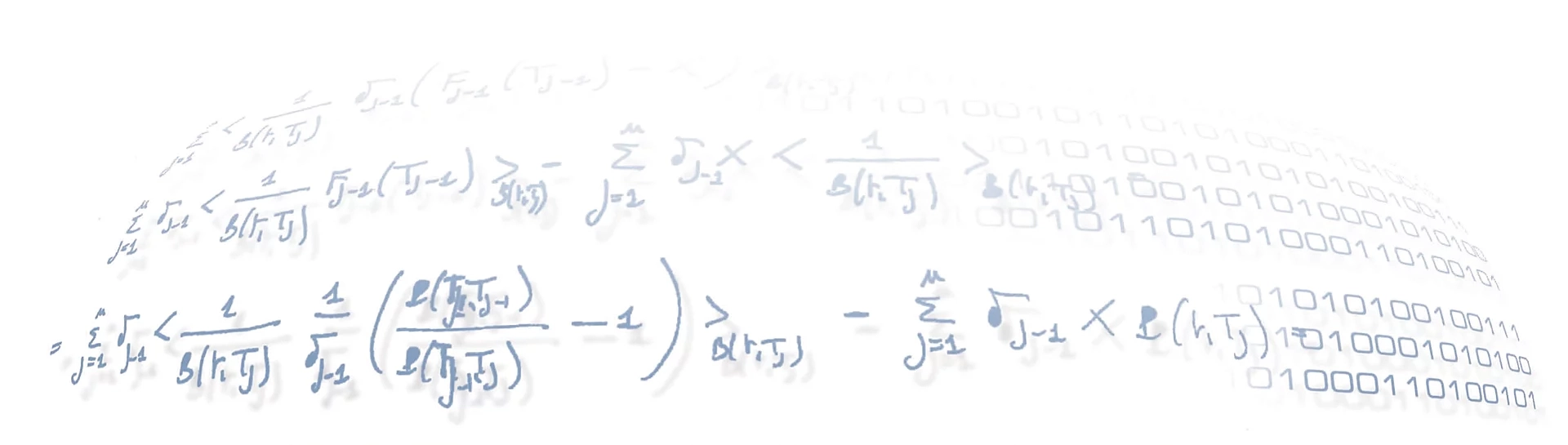1.1 The Framework: Optimal Order Execution

The problem of optimised trade execution is a critical issue faced by participants in financial markets, such as banks, institutional investors and hedge funds (see Almgren and Chriss, Bertsimas and Lo or Cartea and Jaimungal). The goal in this problem is to find the optimal strategy to execute a big order within a fixed time horizon, trying to minimize transaction costs, risk and market impact.

The crucial question that the market participants have to deal with when executing an order is the search for a balance between price impact and opportunity cost. Price impact arises when large volumes are traded, which may produce significantly adverse price movements; moreover, in this situation the traders may decide to act in order to take advantage of price changes. Therefore, for the purpose of avoiding price impact, investors usually break up their large trades into smaller child orders to be executed over a longer period, e.g. during the course of a day or several days. The execution at unfavourable prices, however, can also be due to external adverse market movements between the time of the trading decision and the order execution (opportunity cost).

Another issue that the market agents come across is to find a good compromise between the speed of execution and the prices obtained for the executed shares. A slow trade can expose them to unknown market fluctuations, while a quick one can result in disadvantageous prices. In order to establish whether a trade is convenient or not, execution prices are commonly compared to benchmark prices, such as the volume-weighted average trade price of the day (VWAP analyses) or the midpoint of the bid/ask spread at the time the order was first created (implementation shortfall analyses).

The data a trader has at his disposal are the real time buy and sell limit order prices and volumes, i.e. the so-called limit order book. These data might be of great utility in that they may help make short-term predictions of price movements, evaluate likelihood of execution at a given price, and so on. The large amount of information and the exposition to a variety of market conditions, however, do not make it easy for the agents to determine the best execution strategy and thus requires formulating more or less complex trading models.

1.2 Reinforcement Learning technique

The optimal execution problem has been extensively studied in the literature, traditionally relying on stochastic solutions (see Bellman). However, in many cases, for example in presence of quite complex price models, algorithms of machine learning (ML) are better suitable for the purpose (see Hendricks and Wilcox, Ritter or Nevmyvaka, Feng and Kearns). Here we particularly focus on a class of ML techniques, which is reinforcement learning (RL) (see Sutton and Barto).

In reinforcement learning, agents attempt to learn optimal strategies for sequential decision problems by choosing actions in order to optimise a cumulative ‘reward’. What distinguishes RL from the other ML approaches is that the link between actions and rewards is unknown, and thus must be inferred through repeated interactions of the agent with the environment in which it moves. The significant advantage of this technique is therefore that few input data are sufficient to feed the machine.

In order to help the reader follow the discussion in the subsequent posts, we provide here the basic concepts and specific terminology of reinforcement learning.

The main elements composing a RL system are:

• STATES, discrete and complete representations of the current configuration of the system;
• ACTIONS, what the agent does by applying some policy depending on the current state;
• ENVIRONMENT, the place where the agent moves and interacts with;
• REWARDS, the immediate outcomes of the action performed by the agent in some state;
• POLICIES, the strategies used by the agent for choosing the actions giving the better outcomes.

Imagine you have a cat (agent) and want to teach it to sleep in a specific place in your house (environment): you emulate the situation (state) and the cat can react to it in different ways (actions). If its response is the one you desire, you repay it with some food (reward), on the contrary you shout at it. The result is that, the next time your cat will be exposed to the same situation, it will be scared to perform “bad” actions and respond with the desired action with quite great enthusiasm, looking forward for more food (policy). This is, in a stylized way, how the reinforcement learning works.

1.3 Optimal Execution and $Q$-learning

Among the various RL techniques, the most popular is $Q$-learning, which was first introduced in the PhD thesis of Watkins. This is a model-free algorithm where the agent’s training happens during sequential episodes, by using the environment rewards to learn over time the optimal action to take in a given state.

Many works have employed $Q$-learning to approach the issue of optimal execution, exploiting the relevant features of the order book and the current state of execution in order to select the best action (e.g. child order price or volume) to perform in that state, i.e. the action that allows to minimise the trading cost or, equivalently, maximise the revenue received. These experiments have demonstrated that RL approaches, and in particular $Q$-learning, can provide significant improvements in performance over traditional optimisation policies, and thus are specifically suitable for being applied to the optimal execution problem.

The first extensive empirical application of $Q$-learning to the problem of optimised trade execution in modern financial markets was carried out in Nevmyvaka, Feng and Kearns. In the following blog posts we will present a reinforcement learning model adapted from this work, which we have called for this reason NFK model.