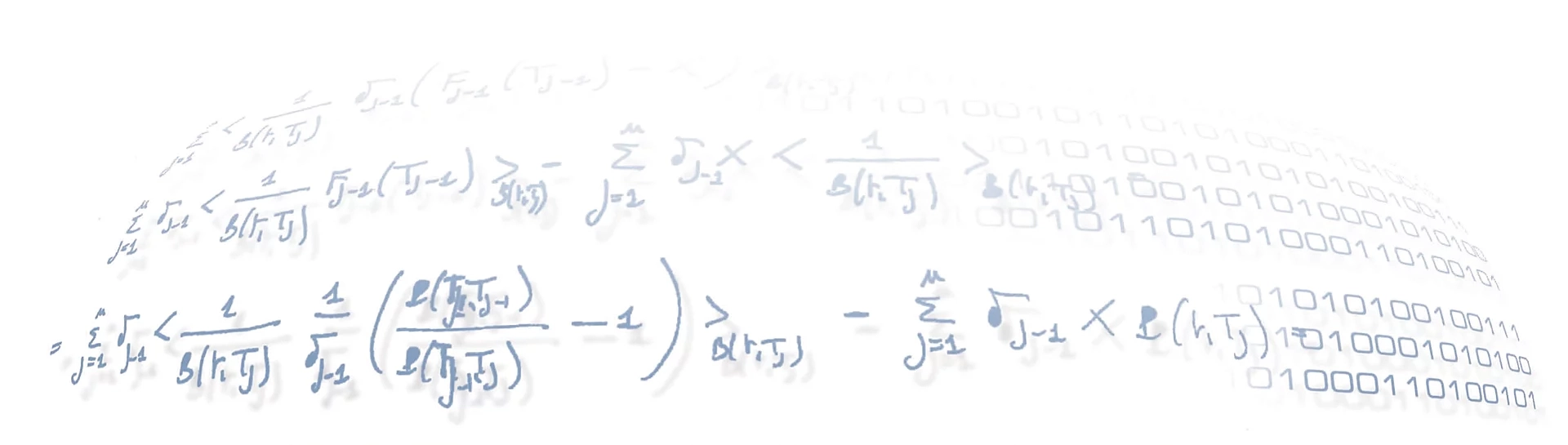1.1 The context

When trading with derivatives, the concept of margin is of primary importance, in that this constitutes the amount of capital which is effectively required to the trader in order to open and maintain a position.

In order to guarantee the successful completion of a transaction, the participants to the market must pay the required margin to the so-called Clearing House, which is an organ representing the automatic and mirror counterpart of all the contracts concluded in the market, and which has the purpose of limiting the default risk of transactions. The extent of this margin is usually of a limited amount and is calculated as a percentage of the unit value of the signed contract.

The required margin is not a fixed amount over time, since the actual value of any position changes continuously according to market conditions. Thus, in addition to the initial margin, namely the amount of funds required as collateral to initiate a position, the investor must maintain in her account an additional maintenance margin as a further buffer; should margin variations exceed this buffer, a margin call would be triggered.

In LIST, the suite of products JANUS has been conceived to monitor risk across multiple assets and near real-time. In particular, one of its functionalities is to accurately replicate the margin evaluation done by the Clearing Houses for portfolios containing futures and options on Equities, Equities Indexes, Commodities, Interest Rates, Energy and FX. If you want to know more about this, you can take a look at the LIST JANUS page.

1.1.1 Margin Minimization problem

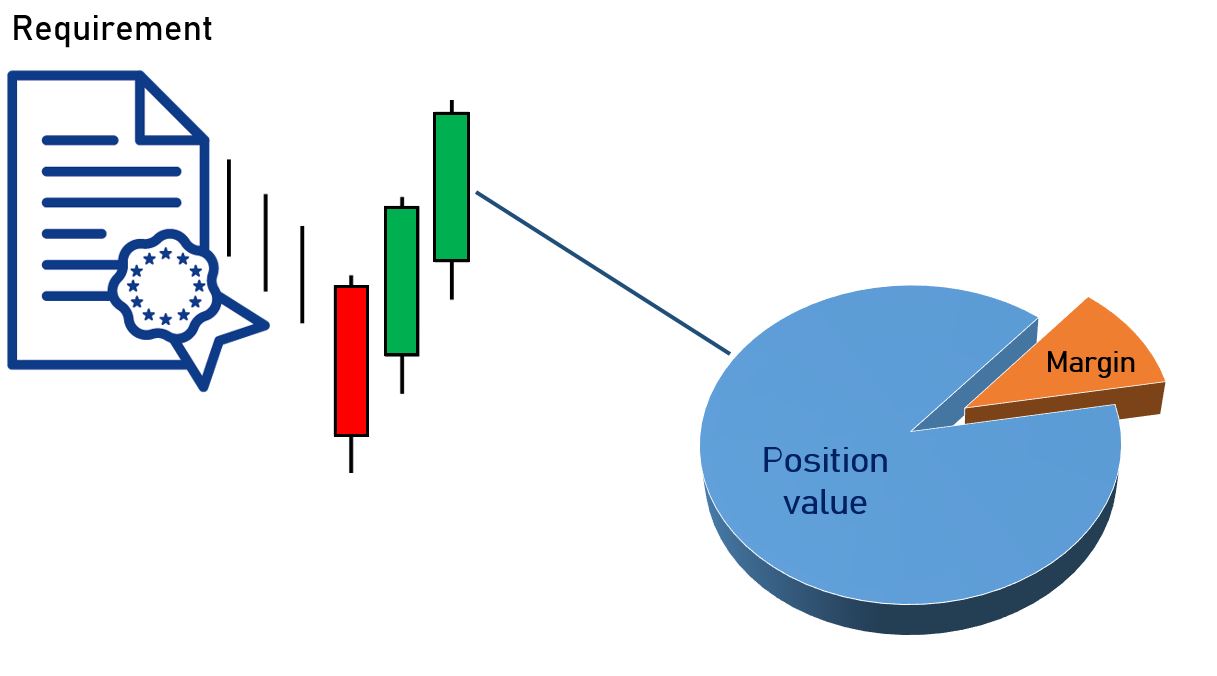
Given an option portfolio, the component (call/put, short/long) positions can be grouped to form definite strategies with a variable number of legs, corresponding to the number of elementary options composing the strategy. Depending on this number, we can distinguish, among the others: spreads, strangles (2-leg), butterflies (3-leg), boxes and condors (4-leg). For each strategy, margin requirements must be satisfied within respectively five business days and fifteen calendar days from trade date (for a complete classification of the strategies and description of the option margin requirements, see the Europe Options Margin Requirements). An explanatory diagram of how margination works is illustrated below, that is, the deposit of a small percentage (orange slice of the pie chart) of the overall value of the trade (blue slice), dictated by the market (candles), is a requirement for the trader to open a position.

Here we consider the strategy-based margin rules established by the Chicago Board Options Exchange (CBOE), which is the largest American options exchange and whose margin regulation methodology has been applied to option customers’ positions for more than three decades (for further details, see the CBOE website).

In this context, a crucial issue is to provide a collection of strategies into which to group all the portfolio options in order to obtain the final required margin. In particular, for a generic strategy the margin is defined as the difference between the “market risk” and the “net option value” (hereafter referred to as MR and NOV respectively) associated with that strategy, where the first one is the risk caused by the future and unforecast variation of option prices and their underlying prices, while the second one is the sum of proceeds from closing all positions. This formula relies on the assumption that the “net option value” is positive for long options and negative for short options. Furthermore, negative values of the margin are set to 0.

Based on the input portfolio, the problem essentially consists in seeking for the “best” collection(s) of strategies covering it, i.e. the one(s) giving the portfolio minimum margin, according to the CBOE indications. This final value is the outcome of netting the individual margins applied to the composing strategies, whose calculation is deterministic and may vary substantially from one to another (as it depends on specific elements such as the option strike price, the underlying price, and so on), ultimately producing a positive or negative result.

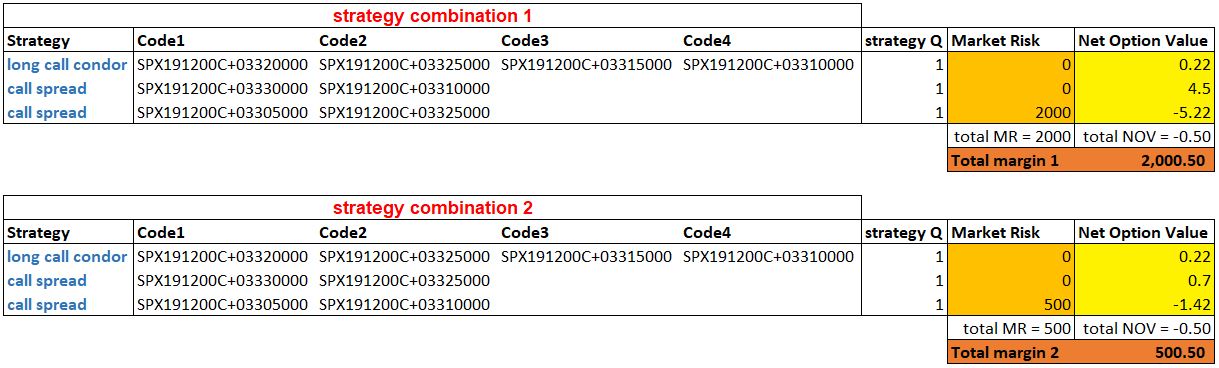
In some circumstances, especially in the case of small portfolios, it may happen that different combinations of strategies lead to equivalent results, i.e. solutions with the same overall margin. However, in the majority of cases the final portfolio risk may change remarkably depending on the chosen strategies, as we show in the numeric example below.

Here it is clear that, even for a simple portfolio (composed of only 6 options), even slightly different configurations of strategies may produce completely diverse margin values (to be intended in currency).

In the light of the above, the search for the minimum margin of a portfolio turns out to be to all effects an optimization problem.

1.2 Combinatorial Optimization approaches

The goal of Combinatorial Optimization Problems (COPs) consists in finding the best solution from a discrete (or reducible to discrete) set of feasible solutions. In many of these problems, due to both their inner complexity and the limited available computing time, an exhaustive search is not practicable and thus the solution cannot ensure the optimality. We refer in this case to heuristic solution methods, which differ from exact methods that in principle can provide an optimal solution. It happens that, in the majority of practical cases, given the specific features of the problem at hand and the need to guarantee tolerable computational times, the quest for a “good” approximate solution rather than an exact one is sufficient, thus justifying the extended use of heuristics in many real applications of a COP.

For this reason, in the last decades the interest for heuristic search methods has consistently grown, and hence a multitude of techniques has been proposed in order to solve a variety of combinatorial problems. As a starting point to the extensive literature available on this subject, you can see e.g. De Giovanni, Blum and Roli, Sörensen and references therein.

In general, a COP belongs to the NP-hard complexity class of problems; thereby, the numerous approaches which have been developed represent specific methods for specific classes of COPs, namely they exploit some special features of the particular COP itself that make it possible to devise some specific heuristics to find a best/good solution.

For instance, Dynamic Programming constitutes a suitable approach when the problem can be simplified by breaking it down into simpler subproblems in a recursive way. More typically, many other techniques can be applicable if the solution space admits some kind of metric that allows to measure a distance between two distinct solutions. In such cases, one can for example employ (Stochastic) Local Search, Variable Neighborhood Search, Simulated Annealing or Particle Swarm Optimization approaches (to learn more about them you can see the references above). Even Genetic Algorithm — inspired by Darwin’s theory of natural evolution and reflecting the natural selection process where the fittest individuals are selected for reproduction in order to produce offspring of the next generation — and Neural Network methods need some solution space metric to be applied.

1.3 The solution proposed and its drawbacks

Unfortunately, in our case none of the aforementioned methods can be employed. Any approach to the problem, in fact, must necessarily select at some point an option-strategy, among the possible ones, as a component of the final solution. However, as soon as an option-strategy is chosen, the remaining solution space — i.e. the list of all the option-strategies still available for being selected — is modified in a radical and non-continuous way with respect to the starting point.

The only operable approach, therefore, is a so-called greedy algorithm of constructive primal heuristics. As an investigation tool, we have implemented a beam search algorithm without backtracking (see again De Giovanni for the details). In particular, the algorithm consists in listing all the possible strategies that can be built from a given portfolio, and then picking one of them on the basis of a specific sorting criterion. Many possible better approaches could be available if only we would be able to reformulate the problem so as to support neighborhood search methods like the ones listed above.

In the following blog post we will present our combinatorial optimization algorithm and describe how it works when applied to the problem of minimizing the risk of an option portfolio.