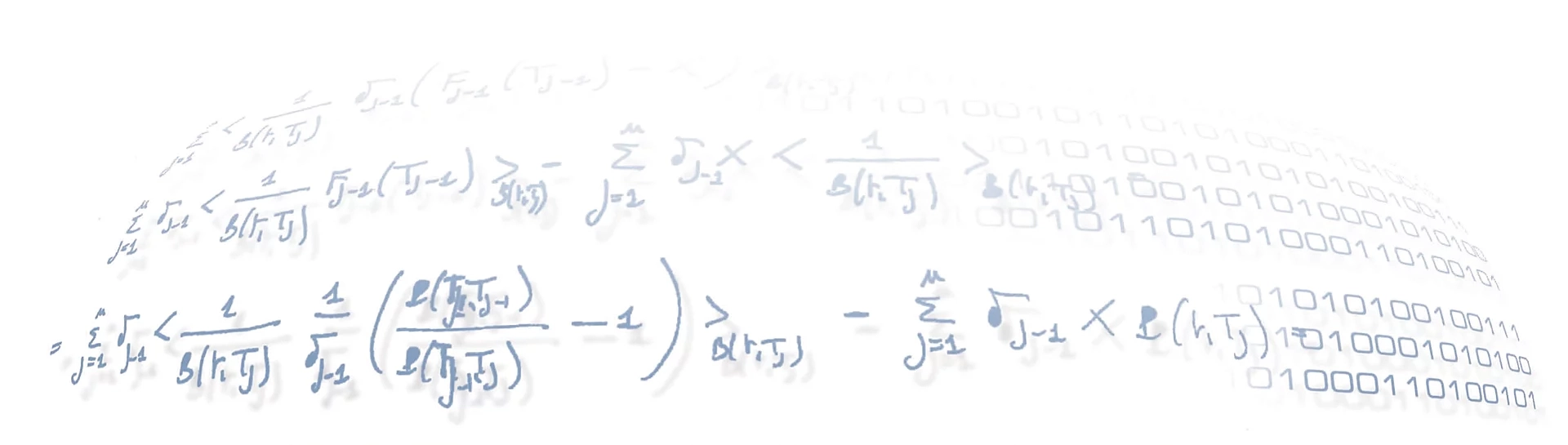3.1 Tuning the remaining hyperparameters

For each particular setup described in the previous sections, i.e. the triplet (user, item, rating), it is necessary to perform a calibration run over the input dataset, namely to apply one of the minimization procedures in order for the RecSys to learn the latent factors and eventually to be able to give a score to any (user, item) pair. Strictly speaking, each particular setup does not exhaust all the hyperparameter selections available, since it remains to be decided:

• the kind of feedback matrix to use (explicit or implicit factorization),
• the dimension of the latent factors space,
• which optimization algorithm to use,
• what kind of loss function to minimize,
• what values to give to specific parameters of the calibration procedure (the regularization constant in the loss function, the various tolerances of the optimization algorithm…)
• etc…

Notice however that whilst the different setups are not necessarily competing with each other, the choice of the other parameters is intended to tune the ability of the RecSys to learn usage patterns. An evaluation metric is therefore necessary in order to compare the different calibrated models and choose the most effective one.

Several standard metrics are available aimed at this purpose. Since, again, the Internet has plenty of resources on these topics, let’s just mention and very briefly describe them.

3.2 The ROC curve and the AOC

A receiver operating characteristic (ROC) curve is quite a generic tool applicable to any binary classification procedure in a supervised learning framework, i.e. where the true classification value is available, against which to evaluate the procedure in question. Namely, by calling

• TP the number of True Positive,
• FN the number of False Negative,
• FP the number of False Positive and
• TN the number of True Negative,

two useful parameters can be define, namely the True Positive Rate (aka sensitivity or detection probability):

• ${\rm TPR} = \dfrac{{\rm TP}}{{\rm TP} + {\rm FN}}$,

and the False Positive Rate (aka false alarm probability):

• ${\rm FPR} = \dfrac{{\rm FP}}{{\rm FP} + {\rm TN}}$,

Usually a classification procedure has a continuous-like parameter, a discrimination threshold that determines the degree of confidence that it must have in order to report a data as positive. So, the ROC curve plots

• the true positive rate TPR on the y axis
• false positive rate FPR on the x axis

for each possible threshold value, allowing to trace an overall performance of the classification model at all classification thresholds.

Graphically, the plot of a ROC curve always starts from the point (0,0) and end in (1,1), and the more the curve is above the straight bisector line from (0,0) to (1,1), the more accurate are the model predictions. This feature of the ROC curve is described quantitatively by the area under the curve (AUC) metric, which is, as the name suggests, the area underneath the ROC curve from (0,0) to (1,1) as a fraction of the unit square area. AUC values ranges from 0 to 1. A model whose predictions are 100% wrong has an AUC of 0; one whose predictions are 100% correct has an AUC of 1.

Let’s specialize this tool in the framework of a RecSys. A general strategy for a backtesting evaluation of the model, is to split the input dataset in two sample: a train sample, over which the model will be trained, and a test sample, that will be used for testing the model in making good rating. In the case of a RecSys, the split is made avoiding that all the interactions of a single user or item are removed from the train sample. If such a thing happens, that user or item wouldn’t be characterize during the training process, and the recommendation system cannot return a rating for it. After training the model on the train sample, the RecSys will try to predict which items the users will prefer based on the data in the test sample. Obviously, for a single user we will recommend only items with which he didn’t have interaction in the train sample. The classification threshold is the length of the recommended list for a single user, and we label the items in this list as positive items, while the others are the negative items. Therefore true positive are the items that showed up in the recommended list and also had an interaction with that user in the test set, while false positive are the items in recommended list that didn’t have an interaction with that user. False negative are the items labeled as negative that had an interaction with the user, and true negative are items that either are labeled as negative and didn’t have interactions with the user. Varying the number of items in the recommended list we can plot a ROC curve for a single user. An overall assessment for the RecSys can be obtained by averaging the ROC curves of all the individual users.

3.3 Precision at k and Recall at k

Precision and recall are classical evaluation metrics in binary classification algorithms which could be translated in the framework of RecSys. Let’s take the list of the top k items recommended to a user, where k is an integer. With the same definition of the paragraph above, precision at k is defined as:

$p_k = \dfrac{{\rm TP}}{{\rm TP} + {\rm FP}}$,

meaning that it is the proportion of top k recommended items that had interactions with the user in the test set.

Recall at k is defined as follows:

$r_k = \dfrac{\rm TP}{ {\rm TP} + {\rm FN} }$,

meaning that it is the proportion of items that had interactions with the user in the test set that appears in the top k recommended items. Note that the definition of recall at k is the same as the definition of true positive rate.

As for AUC score, one could calculate precision at k and recall at k score for every users in the data set, then taking the mean score to evaluate the precision at k and recall at k of the model.